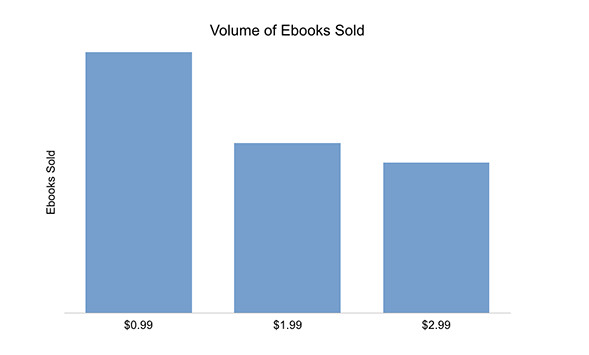
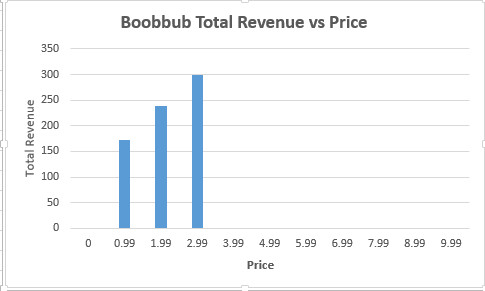
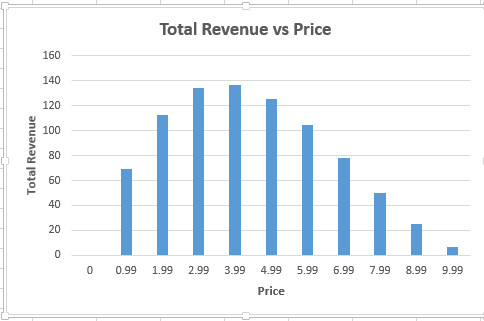
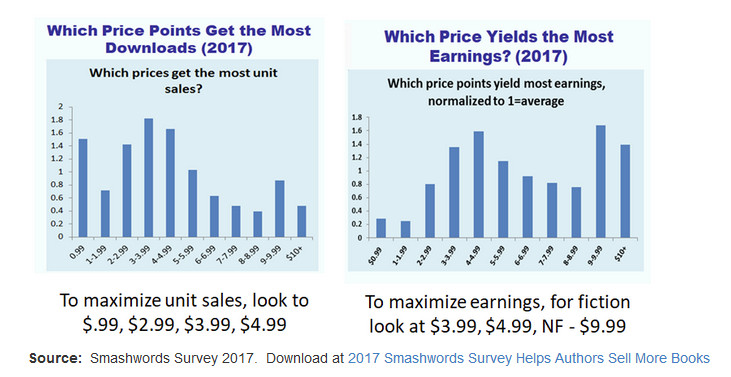
A Typical Street
Briana waited until dawn started to break rather than explore any further in the dark. She was near a gently sloping path paved with large flat and smooth stones. Next to it and a bit lower was a wider surface, dark, and laced with black repairs that looked like giant wandering worms.
Lined up on both sides of the dark surface were rows of what must be carriages for the wealthy. Through glass windows, one could see plush interiors, elegant enough even for a queen. The surrounding shells were smooth steel and painted in bright colors, although some appeared much fresher than did others. For all of them, there was neither purchase for a driver on top nor any means of connecting horses or oxen in the front. And so many! It could not be possible there were so much affluence in one place.
Briana looked downslope, southward if this orb rotated the same way on its axis as did Murdina, in the direction of strange whishing noises that sounded as if a hundred scullery maids were sweeping in unison. In the distance, one of the coaches sped by from left to right, faster than any team of horses could possibly pull. Shortly thereafter came another from the other direction, and then two more from the left.
On top of posts near where they raced were circular lamps gleaming an angry dragon-breath red. After a few moments, they blinked out, and green ones below them began to shine. A screech filled the air, and two more carriages came to a stop on the cross path below. A short time later, a third light beamed yellow and then the red one shown again. When they did, the wagons roared away.
Magic coaches, not one but several. And controlled by imp lamps. Magic and wizardry in blatant display. The exiles had escaped their prison! Not here more than moments, and already she was done. This first adventure was going to be easy!
For confirmation, Briana reached out and touched one of the carriages directly in front of her, but no tingle of magic caressed her fingertips. She shook her head. No, they were not magic after all, and besides, there were too many of them. Better not to conclude in haste. She needed to find out more before she returned home, and she had a day before she could anyway.
Briana started walking southward next to the broader path that she concluded should more properly be called a street or road—for carriages rather than travelers on foot. She touched each vehicle along the way to be sure, but none held any trace of magic.
When she reached the intersection, she noticed there were lamps above the larger avenue cycling on and off also. Although no coaches traveled north or south, the lamps shining there synchronized with those for the east and west. Looking at the signage on shorter poles near the glowing orbs, she mouthed out what must be the name of the larger street.
“Hollywood,” she said, and then the much harder to pronounce, “Blvd.”
The yellow lamp came on and then the red. One of the carriages pulled to the side near where she stood. A door into the interior swung open. A gaunt man who had not shaved in what must have been several days and wearing shabby clothes like those of a beggar leaned across from where he sat and pushed the opening wider.
“I will give you twenty bucks for a quicky,” he said. “How about it?”
A man, Briana thought. Not shrouded like the visitor to the council chamber. Dressed properly, he could pass without notice back on Murdina. And he was speaking in the native tongue. A man. Not an exile.
She felt a moment’s hesitation, even though she had told herself when preparing for the adventure that at some point she would have to speak to the natives. This barter probably was a good a test as any for a first try.
“I. . . do not have a quicky,” she said as she struggled for the meaning of the words. “But I am wondering—”
“Bitch!” The man slammed the door. A loud growl escaped from the front of the carriage as the lamps changed, and it bolted away.
The possibilities expanded. The growl could be that of a demon hiding in the front compartment of the carriage. Maybe the native had been enchanted by the exiles’ sorcery. Maybe the thought about imps in the lamps was still valid.
###
As the sun began its climb into the sky, the road traffic increased in both directions. Briana remained at the street corner, trying to understand what she was seeing. Although still early morning, the number of carriages was far greater than what would be seen in Ambrosia, the capital of Procolon, at midday. She looked both ways down the street. There was no royal palace in either direction that would explain why there was so much rushing about with no apparent purpose.
Her stomach began to growl. The initial excitement of adventure waned, and her energy began to sag. After all, she had been up the entire night.
It was all so kinetic, the scene so. . . so enormous, she thought. Yes, that was the word for it, enormous. She began to feel small, insignificant as a gnat on the back of a djinn. Like a small pebble in a boot that could not be moved out of the way, the thought began to ferment and trouble.
To shake off the feeling, she decided to walk east, hoping a different venue might be more understandable, more representative of the native culture, something she would be able to comprehend.
###
After Briana had travelled for some while along Hollywood Blvd., she began encountering natives coming from side streets and passing her by—more and more, the farther east she went. She felt some apprehension as the first had drawn near, but he did not pay her any heed, nor did any other as they approached.
None of the men were threatening; they displayed neither sword nor dagger. Their clothing was much more colorful and varied than back at home, and thinner rather than practical, the sort of thing young lordlings would strut in order to show off their wealth in the safety of a noble’s court.
The women were the amazing ones. She studied them more intently as they passed. They walked in twos and threes and sometimes alone, all unescorted. And some showed the swell of their breasts for anyone to see. Ladies of the court also did this, Briana knew, but only after the blush of youth had faded as it had for the queen. The younger women on Murdina had no such need.
And their legs! They were bare, some brazenly to above their knees. More astonishing was that they were clean-shaven, as smooth as the face of a man! Those lords who maintained such appearances paid skilled barbers to keep their skins fresh, but certainly, no woman would permit such intimacy by a stranger. That was impossible to understand.
As Briana continued, the structures on either side of the street became taller, some of three stories or more. Not all were simple boxes, but instead looked as if built by drunken masons with tilted and uneven walls. Subdued browns were replaced by a rainbow of colors, sunburst yellows, scarlet-reds, and deep-ocean blues. Large panels of imp lamps danced in intricate repeating patterns, drawing attention to themselves almost as if they were the result of a sorcerer’s charm. Signs were bounded by what looked like alchemists’ glowsticks, but longer and brighter, able to shine fiercely in the daylight. The lamps pulsed on and off in deliriums conveying a mania even more manic than that of the rushing carriages.
Storefronts? Briana puzzled. But far grander than any she had ever seen before. And for none could she recognize what wares were sold. There were signs enough but most with words she did not recognize from her dictionary. And those that she did made little sense. ‘Hard rock’? Of course, they were hard. Why would anyone have to pay for one?
The path on which she walked became grander—wider, darker, and containing an embedded series of white stars blazing the path even though such an aid was not needed. Like a line of marching warriors, tall trees with long naked trunks and plumed with branches at the top sprung out of the smooth stone.
She continued to marvel why no one spoke to her. With her thick tunic, leggings, and pack, she was the one who stood out from the others. But still no one gave her any notice, edging around her, or even jostling her, without a word.
After traversing two more cross streets up ahead, she glimpsed the reason why. There were others dressed the same as she! Some even wore cloaks or capes. Some had masks. Other women in wore sequenced costumes, so short as not to be believed.
They rapidly twirled metal cylinders with white bulbs on the both ends and occasionally tossed them high into the air. Around them clustered others, garbed like the ones who had already hurried past her.
One structure was impressively higher than the two to either side—an entryway built like a helmet worn by a general in a victory parade. It stood at the rear of a large courtyard bare of greenery and underfoot completely covered with a random array of indentations looking like the prints of hands or boots.
Larger carriages came into view, some with seats on the top as well as inside. They pulled to the edge of the street and disgorged their content into the courtyard. The natives that had been discharged ran from one set of indentations to another, obviously delighted, and yelling to others what they had found. It reminded Briana of the rituals of magicians, but here it was too disorganized to have any such a meaning.
As Briana pondered, two young women suddenly surrounded her on both sides. “Selfie!” yelled one and extended a small mirror-like object on the end of a stick.
“What movie?” asked the other. “I don’t recognize your costume. Is it not out yet? Are you one of the stars or only an extra?”
“You are supposed to smile,” the first thrust the mirror in Briana’s face. “Like us. See. Instead, you look like a blank faced idiot.”
“She’s in character, Hester,” the other said. “Don’t you get it? She is playing the role of an idiot.”
The second woman thrust a small book into Briana’s hand along with what looked like some sort of writing quill.
“Well, autograph it,” she said. “Your name, your real name. Who knows? Some day you may be famous, and this will be worth a fortune.”
Briana thought for a moment how her name would be composed in the native’s lettering system and slowly began to make the marks across the page.
“Look at that,” Hester said. “Look what she scribbled. Worse than a kindergartener”.
“That precisely is my point. Like I said. She is in character. Go ahead and give her the tip.”
“This is not worth even a buck,” Hester said. She thought for a moment. “Okay, if you are playing the idiot, you would probably like a nice silver coin, right?”
She reached into a purse, extracted one, thrust it in Briana’s palm.
Briana bristled. Idiot indeed! This was not the way to treat a daughter of Alodar the Archimage. She should. . .
The coin was silver! Maybe. . .
She examined the disk more closely. Her anger had subsided for a moment, but then it returned. Counterfeit! Counterfeit and a bad example at that. It was silver all right, silver overlaid over a copper core. She could see that the baser metal had worn through around the entire circumference.
Briana turned to confront the two women, but they were already moving on through the crowd, looking for additional targets to accost.
It took a while for the heat to dissolve away, but Briana found she could not return to a complete calm. The noise and flashing lights on the storefronts were becoming too much to process all at once.
She needed something to focus on, but the visual bombardment continued its relentless onslaught. Closing her eyes did not help. If she did, the unfamiliar sounds intruded even more. She decided to continue in the direction of a tall tower farther to the east. There, in the distance, the furor of activity seemed to be much less.
But as she did, her discomfort grew. She needed to relieve herself, but no convenient bush or tree was in sight. Her shoulders slumped under the now heavy weight of her pack.
When she reached the tower, Briana looked at the sign across the street. ‘Ripley’s Believe It or Not’, it said. What could that possibly mean? Believe it? Believe what? And if not, then what happened? Her thoughts reeled. Even here, where relatively it was quieter, everything was still too kinetic, too vast, too frenzied, and complex.
The experience was so unlike those recorded in the sagas. When heroes went to an unchronicled land, they coped almost immediately. That would not be possible here. Her original plan of taking a few days to sample the culture was not going to work. It could take a lifetime to figure it all out.
This adventure could be a big mistake. When the portal reappeared tomorrow morning, perhaps she should go home. For a moment, the thought surprised her, but then it rooted, and she had to consider what to do.
Go home? But what would happen then? Be carted off to a grubby fortress in the west? No, she could not do that. She would not do that. Not yet. Not even if many days had to pass. Whatever it took. No return until she had something of value to report.
Her stomach rumbled again. Her tongue was thick in her mouth. She had brought enough sustenance for a few days, but not for how long this was going to take. In addition to puzzling about the existence of the crafts, she would have to take care of the basics too—food, water and a place to sleep. How was that to come about? Could she even eat the food, drink the water? There was nothing familiar here, nothing she understood—nothing she could understand in any reasonable time.
With a sudden jab of fear, Briana realized the predicament in which she had placed herself. The last of her energy ebbed away. She did not want to return, but neither could she stay. She leaned against the wall of the tall building. No one noticed or offered to help as she sagged to the ground. In all of her life, no situation ever had been this bad. There was nothing worse than this.
And as she did, she felt a twinge that rapidly grew into a cramp. She was wrong. It could be even worse. Her time of the month was starting—starting a week early. She had brought nothing for it. And something had to be done now, sooner rather than later. Otherwise, her leggings would have a stain for everyone to see, one that would set and could not be removed.
But by now, she could do nothing. Briana folded her arms over her knees, lowered her head onto them, and quietly began to weep. If the exiles could see her now, she thought, they certainly would be laughing.
Want to read more? Click here
Want to read it all? Click here